|
Anton, Bruno,
Charly, Dennis und Emilio kommen vom Fußballtraining. Als Herr
Klein die Kinder abholt, wird ihm von seinem Sohn Bericht
erstattet:
„Ich habe drei
Tore weniger geschossen als Anton, Charly drei mehr als Dennis,
und Anton fünf weniger als Charly. Bruno hat drei Tore mehr als
ich geschossen.“ |
|
Antonio,
Bruno, Carlo, Dino ed Emilio hanno finito la loro partita di
calcio. Il signor Piccolo che è venuto a prendere i ragazzi
dopo la partita ascolta il resoconto di suo figlio:
“Ho segnato
tre reti meno di Antonio; Carlo ne ha segnate tre più di Dino;
Antonio
cinque meno di
Carlo e Bruno tre più di me.” |
|
Anatolio,
Bernabé, Carlos, Dionisio y Emilio han acabado su entrenamiento
de fútbol. Don Pequeño quien viene a buscar a los niños después
del entrenamiento escucha lo que le cuenta su hijo:
" He apuntado tres goles menos que Anatolio; Carlos tres más que
Dionisio; Anatolio cinco menos que Carlos y Bernabé tres más que
yo." |
|
Alan, Ben,
Charles, Dennis and Eliot's football training session is over.
Mr Small, who comes to get the children after their training, is
being given the report by his son.
"I scored
three goals less than Alan did; Charles three more than Dennis;
Alan five less than Charles and Ben three more than I did." |
Exercice 2
5 points
|
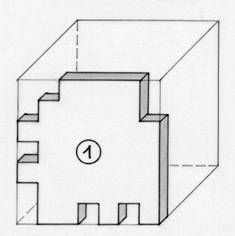
Cube à crans
|
|
|
|
|
Dans une plaque d'épaisseur 1 cm, on a découpé 6
pièces. L'assemblage de ces 6 pièces permet de constituer un
cube d'arête 7 cm.
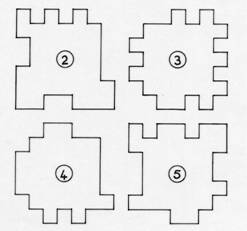
Les
silhouettes de 5 de ces pièces sont représentées ci-dessous. |
Dessiner la silhouette de la 6ème pièce.
|
| |
Exercice 3
7 points |
Près des 1000
|
 |
|
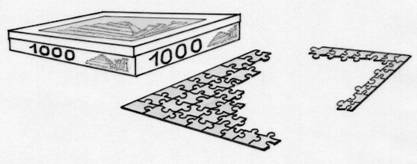
Mélanie veut faire un puzzle. Le couvercle de la boîte
de ce puzzle présente son motif rectangulaire avec
l’inscription : « 1000 pièces ».
La trame du
puzzle, constituée de lignes courbes suivant grossièrement deux
directions perpendiculaires, peut être considérée comme un
quadrillage.
Mélanie met
d’abord de côté toutes les pièces du bord. Elle trouve
exactement 124 pièces de bord, y compris les 4 coins.
En essayant
de les assembler, Mélanie se dit soudain qu’il est alors
impossible que ce puzzle compte exactement 1000 pièces.
|
Quel peut être le nombre exact de pièces du puzzle de
Mélanie, sachant qu’il est proche de 1000 ? Justifier.
|
| |
Exercice 4
5 points |
Pas régulier
|
 |
|
Alain
fabrique un tétraèdre dont les faces sont deux triangles
équilatéraux de 5 cm de côté et deux triangles rectangles. |
Dessiner un patron de ce tétraèdre sur la feuille-réponse.
|
| |
Exercice 5
7 points |
La bonne combine
|
 |
|
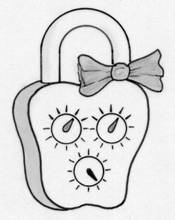
Martine est
bien embêtée car elle ne se souvient plus de la combinaison de
son cadenas.
Celui-ci est
formé de 3 cadrans comportant chacun 12 positions.
Pour ouvrir
son cadenas, Martine décide alors de tester méthodiquement
chaque combinaison : 0-0-0 ; 0-0-1 ; 0-0-2 ; … ; 0-0-11 ;
0-1-0 ; 0-1-1 ; … ; 0-1-11 ; 0-2-0 ; … etc.
Il faut 1
seconde pour chaque test.
Au bout de 16
min 45 s, le cadenas s’ouvre enfin ! |
Quelle est la combinaison du cadenas ? Expliquer la réponse.
|
| |
Exercice 6
5 points |
Platonique
|
|
|
|
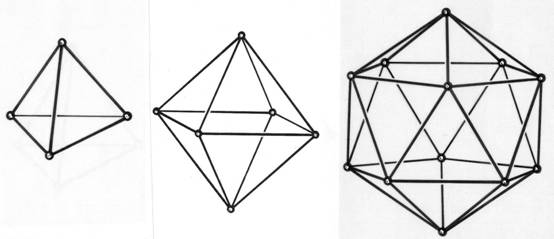
Un jeu de
construction permet de réaliser des maquettes de polyèdres
réguliers par des assemblages de boules métalliques identiques
et de bâtonnets magnétiques identiques.
La maquette
d’un octaèdre a une masse de 132 g et la maquette d’un tétraèdre
a une masse de 76 g. |
Quelle est la masse de la maquette d’un icosaèdre?
Justifier. (voir figure ci-dessous)
|
| |
Exercice 7
7 points |
Prendre de la hauteur
|
 |
|
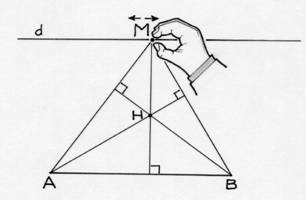
Soit MAB un
triangle de base AB égale à 8 cm. Les points A et B sont fixes.
Le sommet M se déplace sur une droite d parallèle à la
droite (AB). La distance entre les droites d et (AB) est
égale à 6 cm. |
Tracer point par point la courbe
sur laquelle se déplace l’orthocentre H du triangle MAB lorsque
M se déplace sur la droite d.
|
| |
Exercice 8
5 points |
En piste !
|
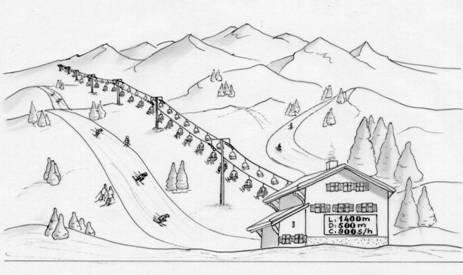 |
| Annabelle est au
pied des pistes de ski et attend son tour pour prendre le
télésiège. Un panneau affiche les caractéristiques du
télésiège :
|
Longueur 1 400 m
Dénivelé 500 m
Débit maximum 900 skieurs / heure
150 sièges de 2 places chacun
|
|
| Le
débit est le nombre de skieurs qui arrivent au sommet en une
heure. Ce débit est maximum lorsque toutes les places sont
occupées à la montée. |
Calculer la durée de la montée pour un skieur.
|
| |
Exercice 9
7 points |
Euro-spin
|
|
figure n°1

|
figure n°2
 |
|
On dispose 6
pièces de 50 centimes d’euros en triangle comme l’indique la
figure n°1. Le mot « Cent »
est écrit horizontalement. On ne déplace que la pièce A en la
faisant rouler sans glisser sur les autres pièces comme
l’indique la figure n°2. Elle reste toujours en contact avec une
autre pièce au minimum. Elle fait le tour des autres pièces
jusqu’à retrouver sa place initiale. |
Représenter les 6 pièces après la manipulation. De quel
angle la pièce A a-t-elle tourné sur elle-même ? Justifier.
|
| |
Exercice 10
10 points |
C'est par où la sortie ?
|
|
|
|
Voici
l’organigramme d’un programme de calcul:
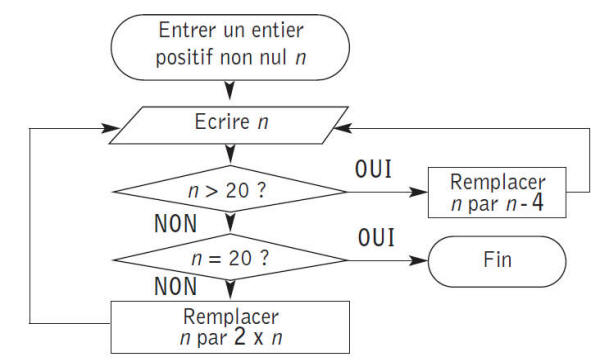 |
Tester ce programme pour n = 11 puis pour deux autres
valeurs au choix.
Ce programme se terminera-t-il quel que soit l’entier naturel
non nul choisi au départ ? Expliquer la réponse.
|
| |
Exercice 11
5 points |
Le b.a.-ba du calcul
|
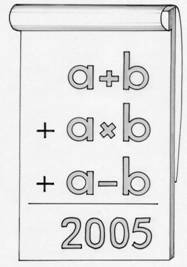 |
Trouver deux entiers positifs a et b, a supérieur à b, tels
qu’en additionnant leur somme, leur produit et leur différence,
on trouve 2005.
|
| |
Exercice 12
7 points |
Oracle à distance
|
 |
|
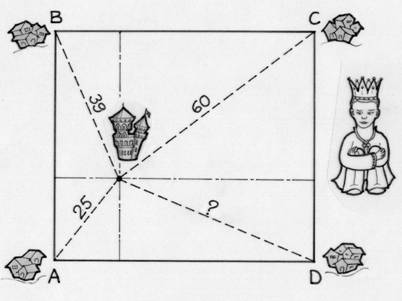
Le royaume du Roi Anselme compte quatre villages A, B,
C, D qui sont les sommets d’un rectangle. Son château est situé
à l’intérieur du rectangle, à 25 km de A,
39 km de B, 60 km de C. Anselme se demande à quelle distance de
D se trouve son château. Pour cela, il consulte son ministre
Gyropathe dont voici la réponse :
Dans quatre triangles rectangles différents,
Un théorème célèbre tu utiliseras,
Les quatre égalités obtenues tu additionneras,
Les termes astucieusement tu regrouperas,
La réponse tu trouveras. |
Calculer la distance qui sépare le château du village D.
|
| |
Exercice 13
10 points |
L'estomac dans les talons
|
 |
|
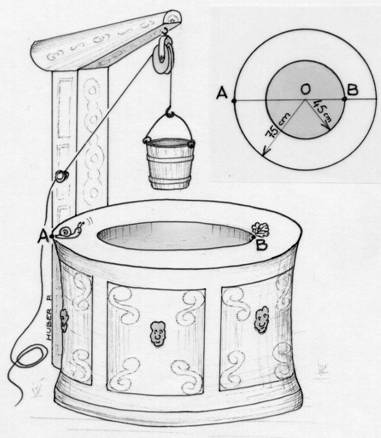
Un escargot
se trouve sur la margelle d’un puits en un point A. Une feuille
de salade est au point B.
Cette
margelle a la forme d’une couronne circulaire de centre O, de
grand rayon 75 cm et de petit rayon 45 cm. Les points A, O et B
sont alignés. |
Calculer, au cm près, la longueur du plus court chemin que
pourrait emprunter l’escargot pour aller manger la salade.
|